Payoff Matrix

What Is a Payoff Matrix?

A payoff matrix is a tool that simplifies decision-making in product management. It allows PMs to analyze, understand, and simplify every branching path of a strategic decision they are about to make.

Originating from game theory, the payoff matrix provides a simple grid overview of all the potential outcomes of your decision-making process by organizing the possible choices and their consequences.

Understanding the Basics of a Payoff Matrix

A payoff matrix is a type of prioritization matrix, which is a visual representation of the outcomes or payoffs of different choices made by individuals in a strategic scenario. It’s a very simple 2×2 (or larger) grid in which you pit two or more possible strategie against each other and inspect every possible outcome.

This is what an empty payoff matrix would look like:

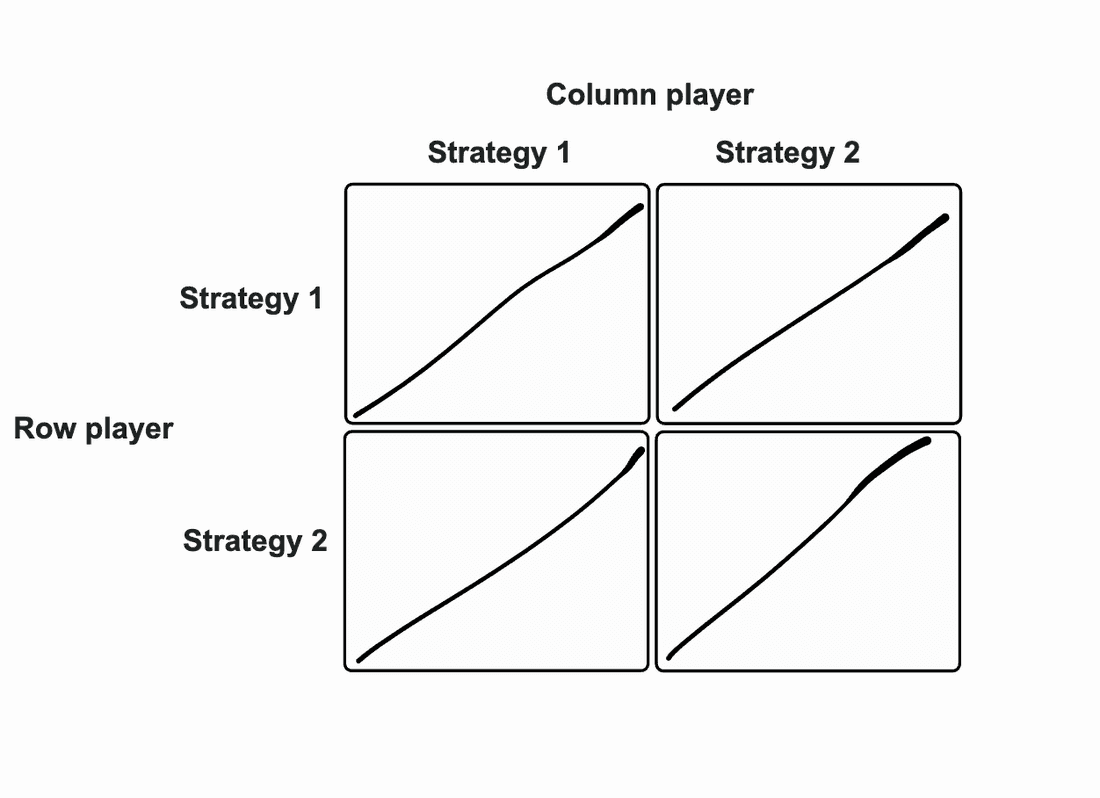
When creating a payoff matrix, there are several key components to consider. In the next section, we’ll cover these components and also see how you can fill in any matrix with ease.

Key Components of a Payoff Matrix

In game theory, a payoff matrix consists of rows and columns (essentially creating priority quadrants) that represent the available strategic decisions for each “player” in any scenario. The entries in the matrix represent the payoffs or outcomes resulting from the combination of choices made by each player.

In short, the key components are:

• Players
• Strategic decisions

Let’s fill in the previous payoff matrix with a mundane example:

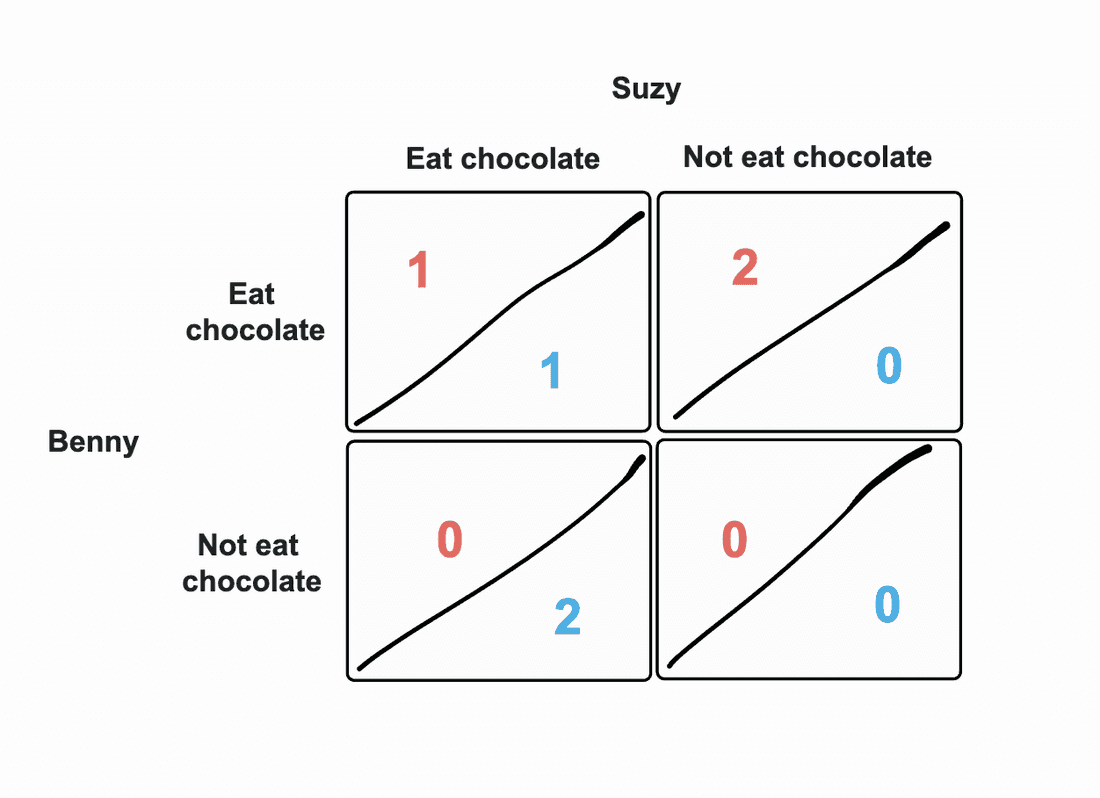
We have two kids, Suzy and Benny.

• The “row” player in our case is Benny, and his strategic decisions are marked with a number in red.
• The “column” player is Suzy, and her strategic decisions are marked with a number in blue.

We bought them two chocolate bars: depending on their choices, they either get to eat 0, 1, or 2 chocolate bars. Reading the matrix is quite simple: if both kids choose to eat chocolate, each gets one; if only one of them wants to eat chocolate, one will get both; and if neither of them wants to eat, they’ll get zero.

Let’s also note that a payoff matrix can take many shapes and sizes, and in some cases, the rows and columns may represent different players or decision-makers, while the entries in the matrix may represent various outcomes or payoffs.

So, prepping the contents (players and strategies) of the payoff matrix is just as important as understanding the logic of the matrix itself. If you are stuck with the former, it’s probably time to learn how to master conflicting priorities.

How to Create a Payoff Matrix

Building a payoff matrix requires a structured approach to represent the different choices and their associated outcomes accurately.

Now that you understand the components, let’s explore the necessary steps to create a payoff matrix.

Steps to Create a Payoff Matrix

1. Identify the two “players” in your scenario. These can be two competing features, your company and a competitor, two major releases, or any two actors.
2. Identify the choices available to each “player” involved in your strategic scenario.
3. Determine the possible outcomes or payoffs resulting from the different combinations of choices made by each player. An outcome-based roadmap can come in handy.
4. Organize the choices and outcomes in a grid.
5. Fill in the matrix with the corresponding payoffs for each combination of choices. This can be any numerical value (potential ROI, download count, market share in $, etc.).

By following these steps, you get a clear matrix that should speed up making the right decision.

And if you need some external help, this handy software development template comes with built-in prioritization matrices and methods.

How to Read Results of a Payoff Matrix

An integral part of using a payoff matrix is interpreting the results it presents. Understanding the implications of the matrix empowers decision-makers to make informed choices based on their strategic objectives.

Whichever players and strategic decisions you have on your matrix, keep in mind that:

• The first number in a quadrant pertains to the row player.
• The second number in a quadrant pertains to the column player.
• It’s not always “the greater the better”: sometimes payoffs come with tradeoffs.
• Your payoff matrix is only as good as the data you use to fill it up.
• Quadrants can have symmetric and asymmetric conclusions (see next section).

Types of Payoff Matrices

Payoff matrices and prioritization matrix criteria can take different forms depending on the characteristics of the strategic scenario at hand.

Let’s explore two common types: symmetric and asymmetric payoff matrices.

Symmetric Payoff Matrix

A symmetric payoff matrix occurs when the payoffs for each player remain the same, regardless of the choices made by other players. In this case, the resulting outcomes are identical for all players (except if there’s a change in priorities).

In the earlier example, Suzy and Benny were given equal choices and thus the payoff matrix is also a symmetric one.

Asymmetric Payoff Matrix

An asymmetric payoff matrix is when the payoffs for each player depend on the specific choices made by other players. The resulting outcomes vary significantly based on the combinations of choices made.

Using our previous example, imagine that Benny and Suzy are given 2 chocolate bars and 2 apples. Suzy doesn’t like apples, though; and suddenly, we have an asymmetric payoff matrix in our hands:

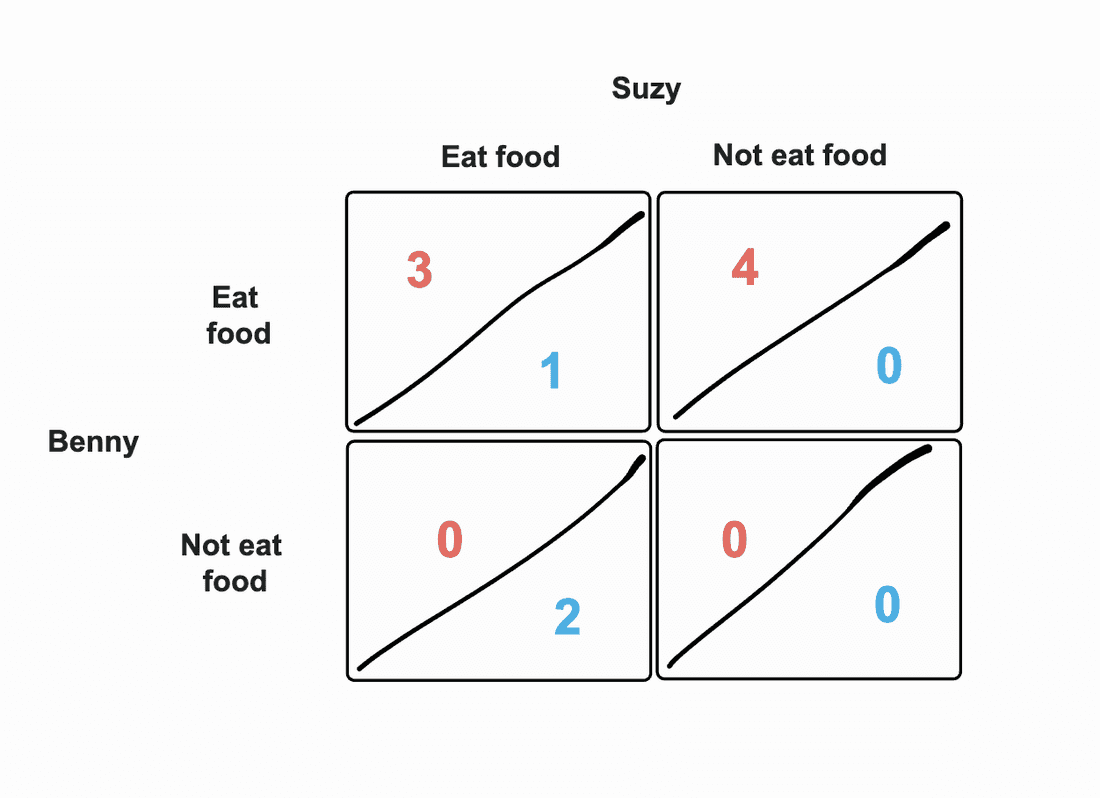
In simple terms, if both of them decide to eat all 4 units of food, Suzy only gets 1 unit of food. Similarly, if Benny doesn’t eat at all, Suzy only gets the two chocolate bars as she detests apples.

Examples of a Payoff Matrix

Now that we got the theory out of the way, let’s see a few more relatable examples of payoff matrices from the world of product management.

Example 1: Music streaming

Imagine you recently joined a startup that competes with streaming giants Spotify or Apple Music. You have a much smaller but loyal user base, and as you plan your next major feature release in the upcoming year, the decision between two options (lossless track quality vs. chat feature) is becoming increasingly more difficult.

For simplicity’s sake, we have two strategic decisions: implement or deprioritize. The numeric value represents the number of users we project to gain/lose:

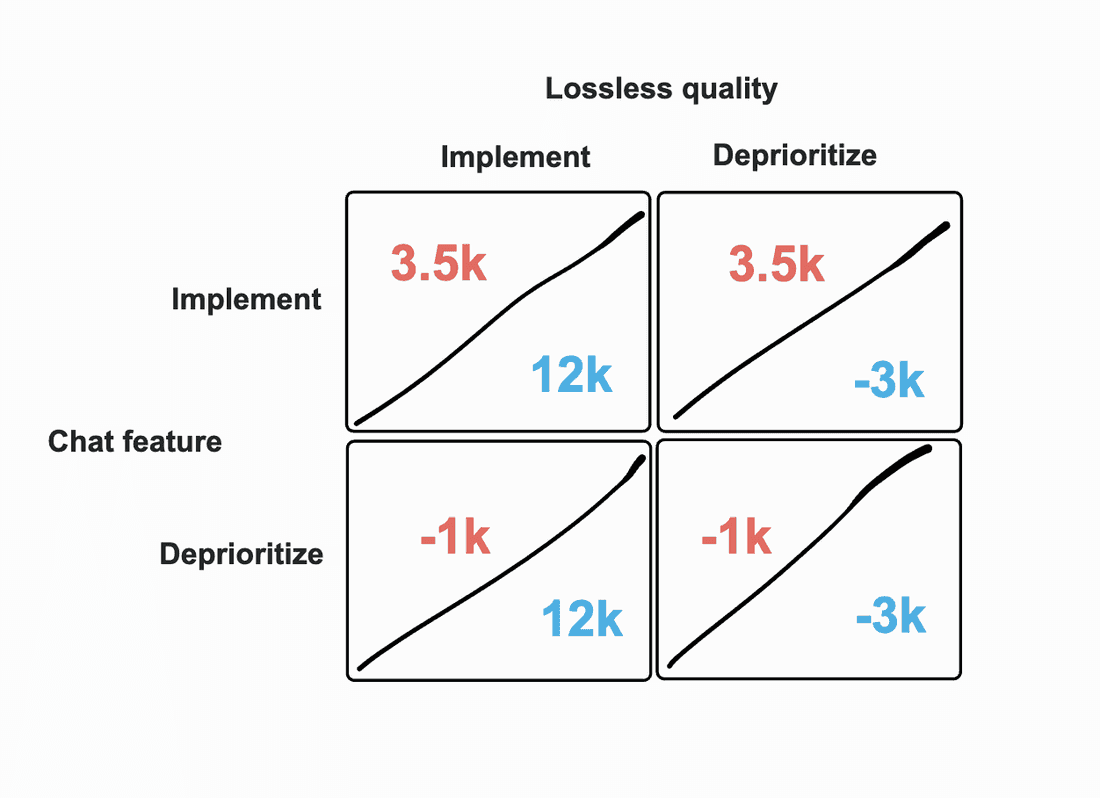
Now, it’s obvious that deprioritizing either of these items will result in a loss of users. Clearly, deprioritizing both of these features makes little to no sense; and, assuming that implementing both is not doable due to capacity issues, the first quadrant only helps us to see the potential maximum we can gain from both features.

This leaves us with the 2nd and 3rd quadrants; and, if we do the math, it’s easy to see that the payoff matrix tells us that we should implement the lossless quality feature and deprioritize the chat feature.

Example 2: Activity tracking

In an imaginary country, two global software companies plan to enter the market of activity-tracking applications. The country doesn’t have any competition, and you have to start creating demand from scratch along with your competitors. You either enter the market with a large budget or a small one and after a lot of planning and gauging interest, you decide to create a payoff matrix to see the potential market share you might gain:

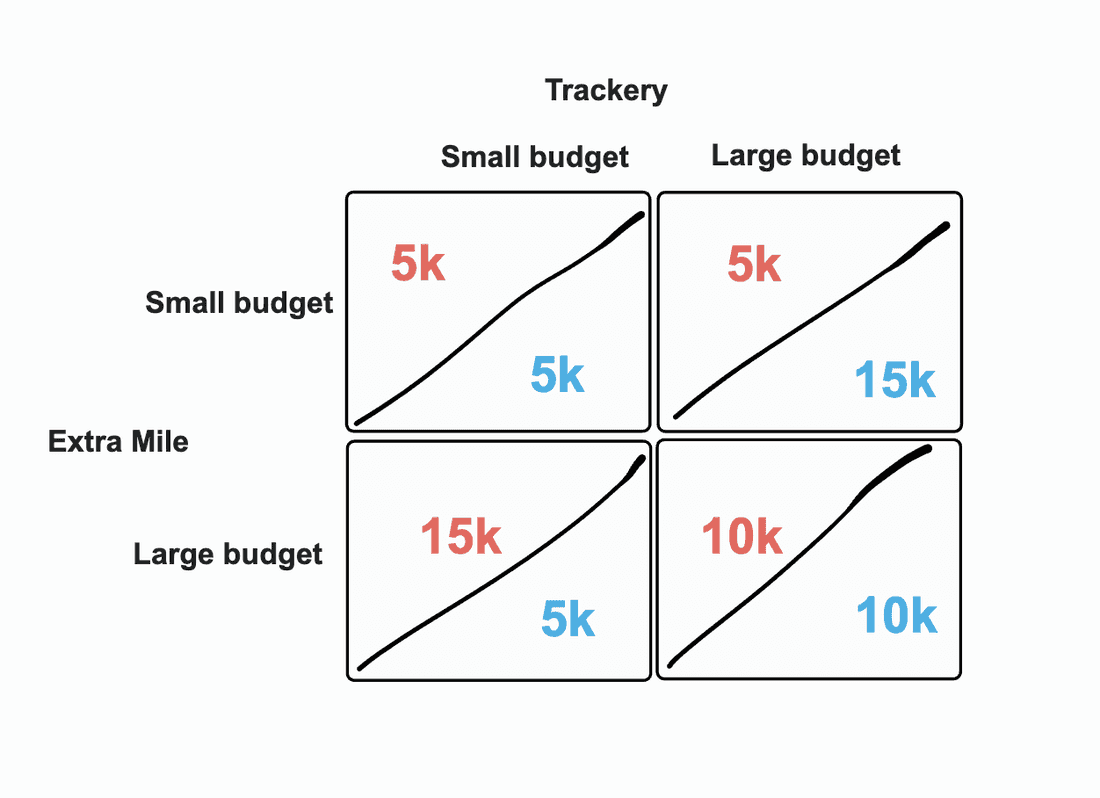
Assuming you both work with the same budget and the available market is roughly 20k users, it becomes pretty clear that sacrificing a large budget yields a huge payoff if your competitor is on a small budget, while if your competitor is on a large budget, you have no choice but to follow suit.

In this example, you both lose out on 5k users compared to quadrants 2 and 3.

Limitations and Criticisms of Payoff Matrices

While payoff matrices offer valuable insights into decision-making processes, they also have limitations and are not without criticism. Understanding these limitations helps you use payoff matrices effectively, recalculate plans, and deprioritize if needed.

Potential Drawbacks of Using a Payoff Matrix

One potential drawback of using a payoff matrix is the assumption of complete and accurate information. In real-world scenarios, information is often incomplete or uncertain, which can impact the accuracy of the payoffs estimated in the matrix.

Just take a look at our previous examples - the streaming one might have miscalculations about potential new users added or the impact of deprioritizing features.

Payoff matrices rely on distinct outcomes and fixed payoffs, and in the real world, you’ll often find more nuanced situations. In our second example, budgets would be hardly known and comparable before entering a market.

Addressing Criticisms and Misunderstandings

To address these criticisms and potential misunderstandings, decision-makers should complement the use of payoff matrices with other decision-making tools and techniques. These can include sensitivity analysis, scenario planning, and real-time data collection to refine the accuracy of the payoffs presented in the matrix.

By combining the insights generated by the payoff matrix with other analytical tools, decision-makers can create a more robust decision-making process.

In Conclusion

A payoff matrix is a versatile tool in game theory that helps stakeholders understand the potential outcomes of their decisions. It enables decision-makers to assess the consequences of different choices, allowing them to make informed and strategic decisions.

While payoff matrices have limitations, they remain a valuable resource in the decision-making toolkit, helping individuals navigate complex scenarios and optimize their outcomes.

If you’d like to build your own payoff matrix (or any other matrix for that matter) and boost your decision-making processes, why not give Fibery a go? Sign up for your 14-day free trial now.