Abstraction and Complexity

Disclaimer: this article mixes painting, poetry, mathematics, data visualization, physics, programming, and other disciplines, smoothly transitioning into software development. Therefore, it’s better for the faint-hearted to skip reading.

Let’s start with definitions

Abstraction is a process wherein general rules and concepts are derived from the usage and classification of specific examples, literal (real or concrete) signifiers, first principles, or other methods.

“An abstraction” is the outcome of this process—a concept that acts as a common noun for all subordinate concepts and connects any related concepts as a group, field, or category.

Here I want to get answers to the following questions:

1. How has the level of abstraction changed in various areas as humanity evolved?
2. What is the connection between abstraction, complexity, and the power of the system?
3. How does this help or hinder us all in software development?

Let’s get started.

Painting

People began to depict various things quite a long time ago. Hunting scenes, fishing, and groups of people with sticks were particularly in demand. Gradually, painting evolved and became more technical. Different genres emerged, which we will discuss.

Realism

In this genre, artists paint the world as they see it. Everything is very specific. There are fictional plots, but overall it’s quite clear what the artist has depicted and what they want to say.

Everything in Perov’s painting is quite specific. Three hunters are engaged in an exciting conversation. The topic of their conversation is unknown to us, but we can assume that the hunter on the left is describing a thrilling encounter with a bear/boar/tiger, which the central hunter seems somewhat skeptical about.

Everything is clear. No abstractions in sight.

Impressionism

The real world passes through the artist’s consciousness and blends with their personal sensations and impressions. It’s no longer simple to understand what is depicted in the painting.

The blurred silhouettes of the harbor, a strange combination of colors, and a dollop of uncertainty. At that time, critics were quite harsh about impressionist paintings. For example, they said, “Even wallpaper would look more finished than this ‘Impression’!” Now, everyone loves the impressionists.

Abstractionism

Abstract art attempts to move away from the direct representation of reality entirely. The artist’s consciousness and his view of the world come to the forefront.

On the one hand, we see simple rectangles of different colors and sizes. On the other hand, the scope of interpretations of the painting is vast. Some may see in it the stained glass of a Catholic cathedral, others the execution of Charles I, and yet others an irregular line on the left. Here, a higher level of abstraction increases the power of the system.

Abstract art is not to everyone’s liking. Many people do not understand it.

Poetry

Similar processes can be observed in poetry. As civilization developed, increasingly abstract genres began to appear.

Realism

Let’s start with a literal epic. A snippet from The Poetic Eddas:

The Valkyrie spake:
8. "Swords I know lying | in Sigarsholm,
Fifty there are | save only four;
One there is | that is best of all,
The shield-destroyer, | with gold it shines.

9. "In the hilt is fame, | in the haft is courage,
In the point is fear, | for its owner's foes;
On the blade there lies | a blood-flecked snake,
And a serpent's tail | round the flat is twisted."

All is quite concrete and clear.

Impressionism

Federico García Lorca usually wrote not-so-straightforward poems. For instance, the poem Crossroads:

East wind,
a street lamp
and a dagger
in the heart.
The street
quivers like
tightly pulled
 string,
like a huge, buzzing
 horsefly.
 Everywhere,
I see a dagger
in the heart.
1921

The interpretation is no longer so easy. There’s an inkling of anxiety on the city street and a sense of dead-end. Interesting comparisons and images emerge. There’s no clear description here, rather just a mood.

Futurism

The further we go, the less certainty we encounter. Let’s take early Mayakovsky and his poem Could You?:

I promptly smeared the map of daily
With splashing paint in one quick motion
I have displayed on a tray of jelly
The slanted cheekbones of the ocean
Upon the fish scales’ tinsel pattern              
I’ve read unknown lips’ salute
 And you,
 could you have played
a nocturne
On a waterspout for a flute?
1913

And let’s consider a couple of possible interpretations of this poem. I will only provide brief excerpts:

The ”map of daily”, a leaf of our life with daily, identical worries, where road schemes, building locations, objects are already pre-drawn by someone. And Mayakovsky “immediately smeared” it, did not flood, did not stain, but specifically mixed irrevocably, without looking at the consequences “splashing” an entire glass of paint. He changed his life, abruptly, recklessly, renouncing the old, like a person thirsting for a revolutionary explosion.

And another variant, which personally seems to me much closer to reality:

Mayakovsky, waiting for good weather, orders aspic with wine in a fish restaurant, clumsily overturns the latter, and here comes the poem, about which non-stop debates are still going on.

Raising the level of abstraction again gives us a firework of interpretations. So what did he want to say with this? We’ll never know for sure.

Mathematics

Let’s move on to more precise sciences. Mathematics itself is quite abstract, so let’s take something simple—numbers.

Natural and rational numbers

It all started with the need to count the number of attacking wolves and compare them with the number of defending people, so natural numbers are counting numbers: 1, 2, 3, 4, and so on. It should be said that the number 3 is quite an abstract concept in itself. In fact, it does not exist in nature. There are 3 trees or 3 sheep, but there is no number 3.

Then the wise Indians invented the number zero. For a long time, 0 was not considered a number in Europe, but some kind of conditional symbol. Even in the 17th century, there were gentlemen who did not want to acknowledge zero. Negative numbers were introduced for convenient recording of debts and solving some equations. The result was whole numbers: -2, -1, 0, 1, 2.

Everything would be fine, but sometimes you want to measure something. For example, the length of a segment. Whole numbers will not be enough for this. In fact, if my reference segment fits in another segment more than 1 but less than 2 times, then what is the length? Fractions come to the rescue. We divide one segment by another and get a fraction n/m. Such numbers are called rational.

Irrational numbers

Further on it gets complicated. It turned out that some numbers can’t be represented by fractions. For example, the number “pi”, or the square root of two. This fact boggled the minds of the ancient Greeks who carefully ignored such numbers. They are called irrational numbers. Giving a precise definition turned out to be quite tough—luckily, Dedekind succeeded at it.

Irrational numbers are much harder to imagine than whole numbers. Indeed, what is Pi?

Complex numbers

But that’s not all. We have reached complex numbers, which are described in the form z = x + iy, where i is an imaginary unit. Fortunately, in our enlightened age, complex numbers are taught in school. But, unfortunately, only about 5% of students understand them.

What do we have? Complex numbers are the most abstract and the most powerful. From them, all other numbers can be derived. In addition, they are the most difficult to understand.

(We won’t touch on even more abstract quaternions, octonions, and sedenions, because I don’t know them well and if you’ve made it this far, I’d like you to stick around).

Physics

In physics, there’s a plethora of examples of raising the level of abstraction. Let’s take the simplest one: gravity.

At first, it was just observed. You take a stone, let it go, and for some reason, it falls to the ground. Galileo was dropping balls. This is the lowest level: the observation of a specific phenomenon.

Newton’s law of universal gravitation

Then Newton took everything and generalized it. He not only concluded that all bodies are attracted, but also derived the dependence: the product of masses divided by the square of the distance between the bodies. Suddenly it became possible to describe the movements of planets, comets, and other celestial bodies. The interaction propagates instantly, and everyone is happy.

General theory of relativity

Unfortunately, gradually some phenomena were discovered that did not fit into Newton’s neat and beautiful theory. One such caveat was the precession of the perihelion of Mercury (an extremely intriguing story of attempts to explain this phenomenon). It would seem that photons have no mass, so light should not be deflected—yet it is deflected. To eliminate this and other larger contradictions, the general theory of relativity was introduced. It postulated the maximum speed of interaction propagation (the speed of light) and the connection of space-time with mass. Light actually travels in a straight line, but space near the sun is curved.

The general theory of relativity takes the explanation of gravity to a new level of abstraction and is completely inaccessible to the vast majority of the world’s population. It also includes Newton’s theory as just a special case. And of course, it is much more powerful, as it can explain and predict the existence of a much larger number of phenomena.

Functional Programming

Let’s briefly scratch the surface here, without delving into category theory.

Variables

The most primitive level is assignment, for example var n = 1. An abstract symbol like n will be equal to 1. It’s all quite simple.

Functions

Next, we have functions f(x) → y. We take a value of some type as input, and we return another value of a different type. For instance, this function adds one:

function addOne(a) {
  return a+1;
}

With the use of functions, we can properly program, break the solution down into subprograms, and use them in different places.

Higher-order functions

We take the level of abstraction up a notch and introduce higher-order functions. Here, we can already take other functions and return functions f(g(x)) → h(x). The system’s power increases at this point, and we can do cool things. Note that some functions are similar and write more abstract functions.

For instance, multiplying each element in a list by 2 and converting a list of numbers into a list of strings—these are all a map operation over a list, just with different parameters. We write such a function once (abstracting from what exactly happens to the list element), and then higher-order functions help us to perform different operations with its help.

function map(xs, f) {
  var acc = [ ];
  for (let x of xs) {
    acc.push(f(x));
  ｝
return acc;

We create a lot of such abstract operations over lists (map, filter, group, skip, take, etc.), and then we notice that actually all of them can be implemented through an even more abstract function reduce/fold.

function map (xs, f) {
  return reduce(xs, (acc, x) => acc.push(f(x)), [ ]);
｝

function filter(xs, f) {
  return reduce(xs, (acc, x) => {
    if (f(x)) {
      acc. push(x);
    ｝
  ｝，[ ])；
｝

function reduce(xs, f, seed) {
  var acc = seed;
  for (let x of xs) {
    acc = f(acc, x);
  ｝
  return acc;
}

And then we see that this reduced operation can be applied not only to lists but to anything that has some structure (for example, a tree). Here we encounter the type class Foldable, which defines methods like fold. If an object instances this type class, defining its own fold implementation, then such an object can immediately be used with operations like map/filter/etc., which were previously defined through reduce.

Elevating the level of abstraction again gives us even more powerful solutions.

Data Visualization

People have been trying to present things beautifully for quite a long time. But previously, there was less data, so mainly maps were used. Then, data gradually started to emerge and clever gentlemen from different countries began to invent diagrams. Scotsman William Playfair was particularly outstanding: he invented three diagrams.

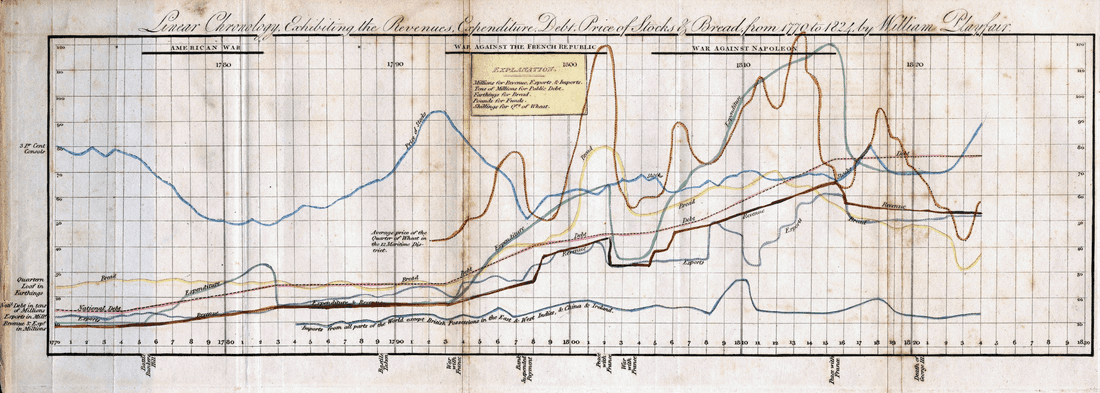
Charts Library

Over time, more and more types of charts were invented, common patterns were identified, and everything was standardized into a chart library that any Excel user would be familiar with.

It seems like this is all, right? Of course not! Jacques Bertin performed a small feat by writing the magnificent book Semiology of Graphics. He summarized the principles of data visualization construction and opened the path to a completely new level of abstraction, which not only includes all known existing diagrams but also allows for easily inventing new ones.

Grammar of Graphics

Bertin’s ideas were further developed by Leland Wilkinson, who created the Grammar of Graphics. In short, each diagram consists of the following elements: Data, Algebra, Scales, Statistics, Geometry, Coordinates, and Aesthetics. And we can combine them to get practically any diagram. For example, facet diagrams are described extremely simply:

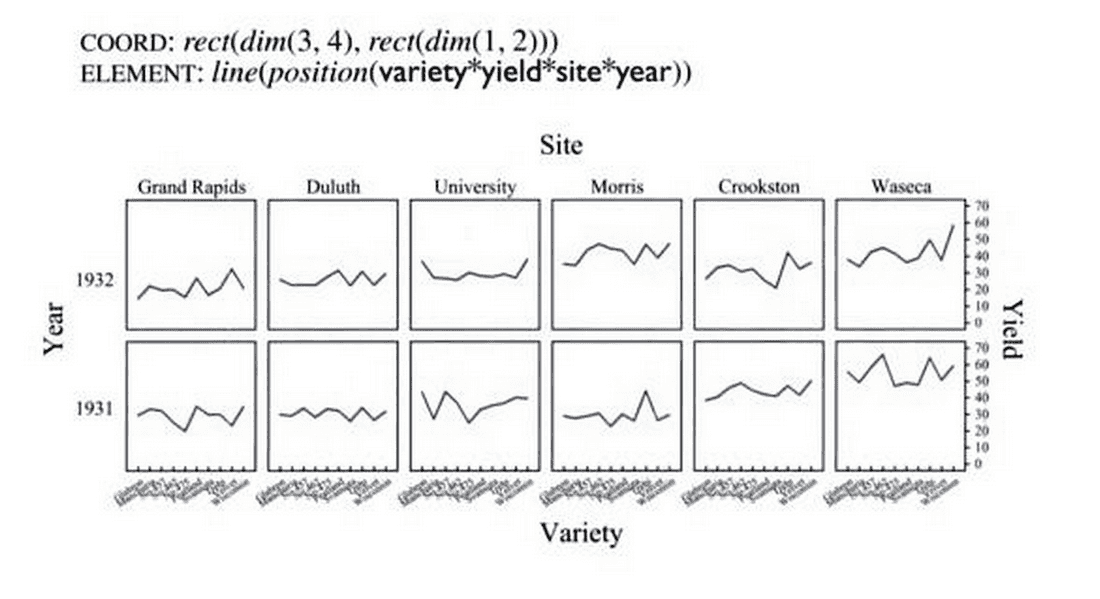
With this grammar, any diagram can be created. However, it’s not free: the grammar is quite complex and takes time to master. If you want to see how Grammar of Graphics looks in action, check the ggplot library.

As we can see, solutions in this field are becoming more and more general and powerful.

User Interface

Let’s move to much younger and less-studied domains. Can we generalize the user interface, and make it more abstract?

Custom UI for a single use case

The lowest level is the specific solution to a specific problem. For example, we need a bug list, so we create a separate screen that only solves this task.

Every screen in the system is unique in some way. Of course, there are common principles. But overall, these are separate pages with their own code.

Generic UI component

The question arises: is it possible to solve the task of creating a list of anything from scratch? Can we create such a universal list, based on which we can create the screens we need? Generally, this is possible. We need to properly decompose this data representation and come up with the ideal solution for each component. The list consists of columns, actions, hierarchy, pages, filters, editing, and so on. The task of creating such a universal UI component is quite complex but feasible. For example, AG Grid is quite a generic component that can be used for many use cases.

UI components library

Over time, I concluded that almost any Enterprise application can be assembled from a finite set of high-level UI components. In general, any Enterprise application visualizes data and allows you to work with it, preferably interactively. The set of UI data representations is finite, and that’s good. So far, I think it looks something like this:

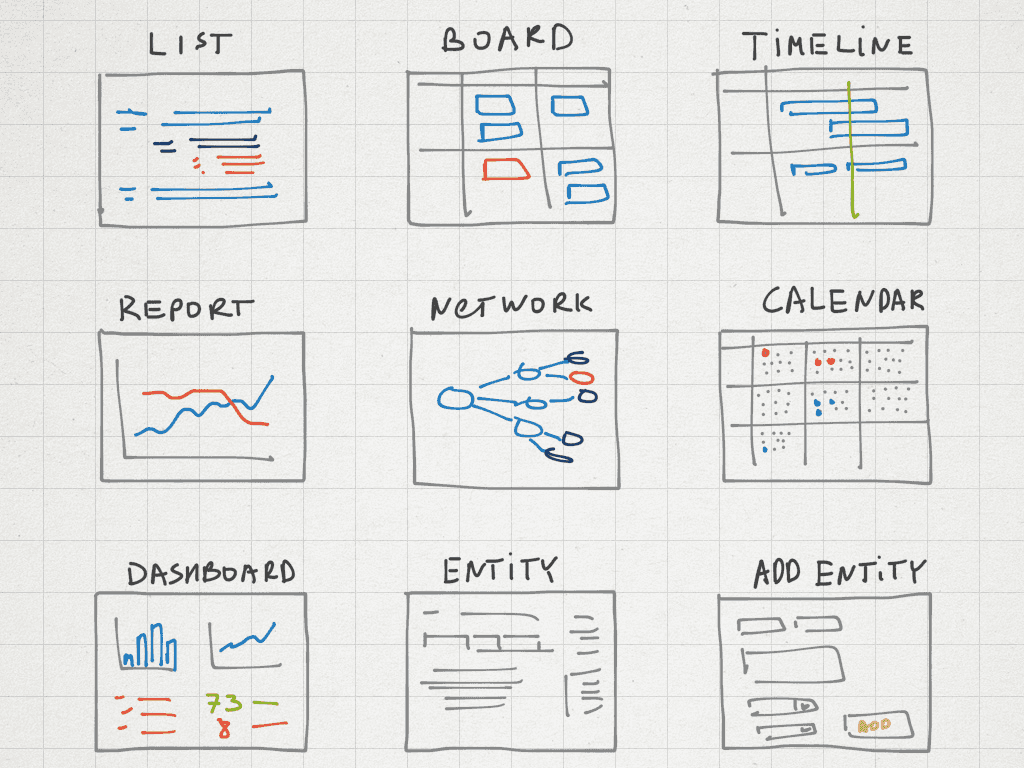
Of course, there are unique screens with various settings, administrative tricks, and so on. But all the data work, which is the main part of the application, can be implemented using a dozen common components. In an ideal world, by implementing these components, we can quickly churn out project management systems, CRMs, Service Desks, and other solutions. I think Targetprocess was the first tool that introduced this idea around 2010. Recently many tools adopted this way of thinking, including Notion, Airtable, Fibery, etc.

Can we have something even more abstract? Maybe some kind of UI grammar? Maybe, but I have seen no progress in this area so far.

Enterprise Applications

Let’s talk about enterprise apps.

Custom Development

The most specific level is custom software development. In this case, a company solves its problems in the most specific way with the help of software developers. The advantages are obvious: a custom-made suit often fits better. But if the tailor is bad, it’s not guaranteed. The disadvantages are also clear: it’s very expensive and not fast.

Usually, in custom development, developers do not bother much with scalability, focusing more on the speed of development. So, after a decade, a system usually turns into a big ball of mud and nobody wants to touch anything inside (for a good reason).

Products

Most niches are filled by products, which can be slightly adjusted to fit one’s needs. Unfortunately, there are problems with the extension and customization of existing products:

1. There are usually quite a lot of restrictions on the product and it’s impossible to get a suitable solution even with customization.
2. Complex customizations need developers, so it’s not the cheapest solution either.

It turns out that companies often replace products every few years, always settling for a less-than-perfect solution.

So what’s the ideal Enterprise application? It has to adapt to any company without the involvement of programmers.

Imagine that you are choosing software for project management and you are told the following:

First, we need to find out how you work. Then we help you install and configure the system exactly the way you need. It will have only the entities you need, with the necessary properties and rules, in the terminology you are used to, only useful screens and nothing superfluous.

Is this possible?

Domain Grammar

I believe we need to invent a form of domain grammar. It could consist of something like the following:

• Entities: we can create any entities with any fields.
• Relations: entities can be linked to each other.
• Metrics: any metrics can be calculated in the system. For example, project progress is calculated very differently in different companies.
• Rules: any rules can be defined in the system. For example, close the task if all bugs and all subtasks are closed. Rules in different teams are very specific.
• Events: use of events for notifications of external and internal systems, communication channels, and so forth.
• Actions: actions can be defined in the system on entities: merging, changing type, deletion, etc.
• Workflow: flexible configuration of states of any entities.
• Permissions: setting access rights to any entities and fields.

By creating a system where you can declaratively describe a business domain, and tying it to the UI components library (see above), you can achieve a near-ideal solution for a vast number of enterprise applications. Even by creating such a system in one domain, for example in project management, we can and will come up with a unique solution at a new level of abstraction and power, which will completely change the market.

Creating such a system is an extremely difficult task. It is worth spending 15+ years on it. I already spent 7 and not even sure I’m halfway there.

Conclusions

Here’s a summary table for all the areas we have examined. On the left, we have specific things, and on the right — quite abstract ones. Things in the left column are easy to understand, while things in the right column are much harder to grasp.

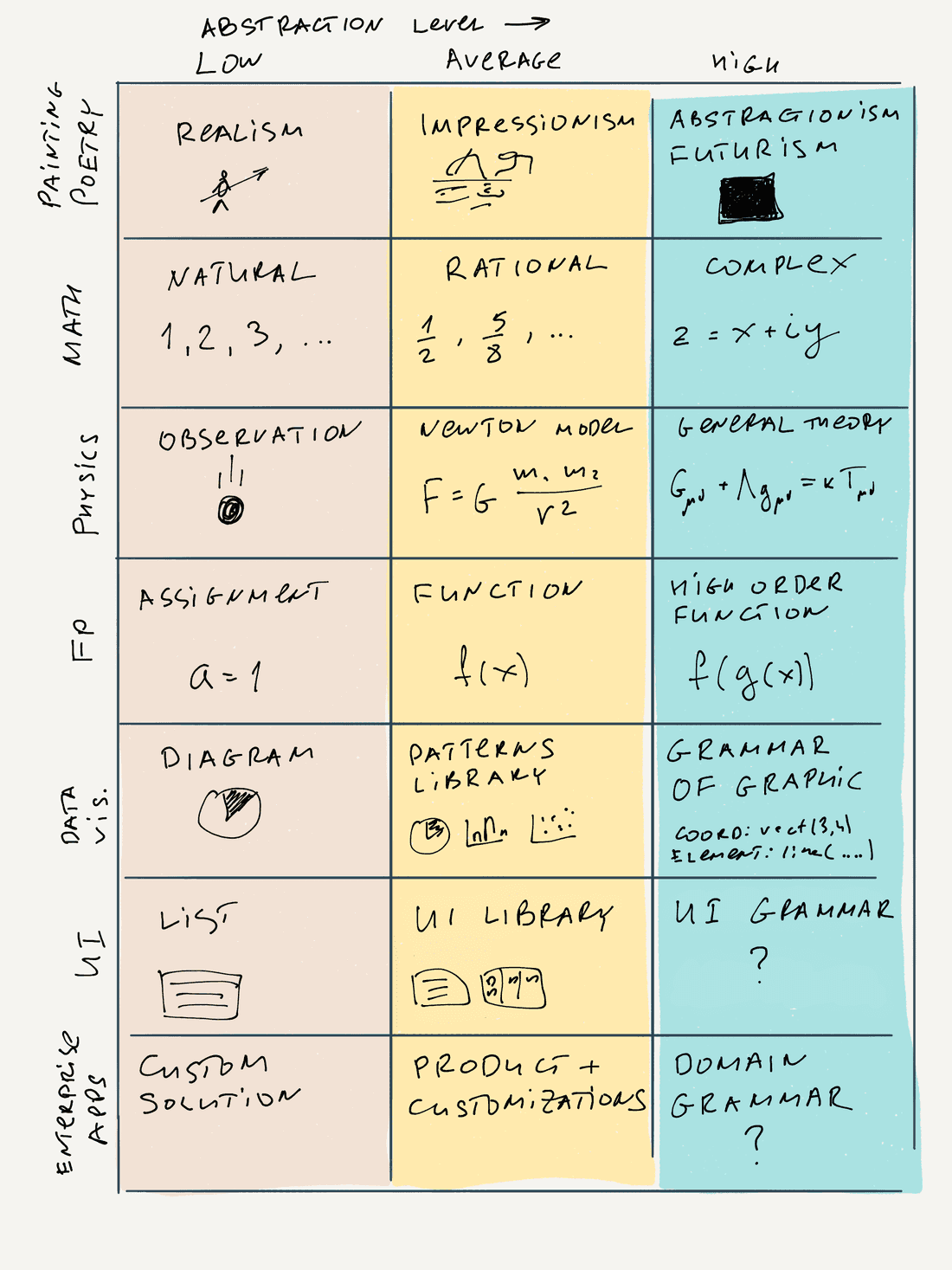
The time for synthesis has come!

Complexity

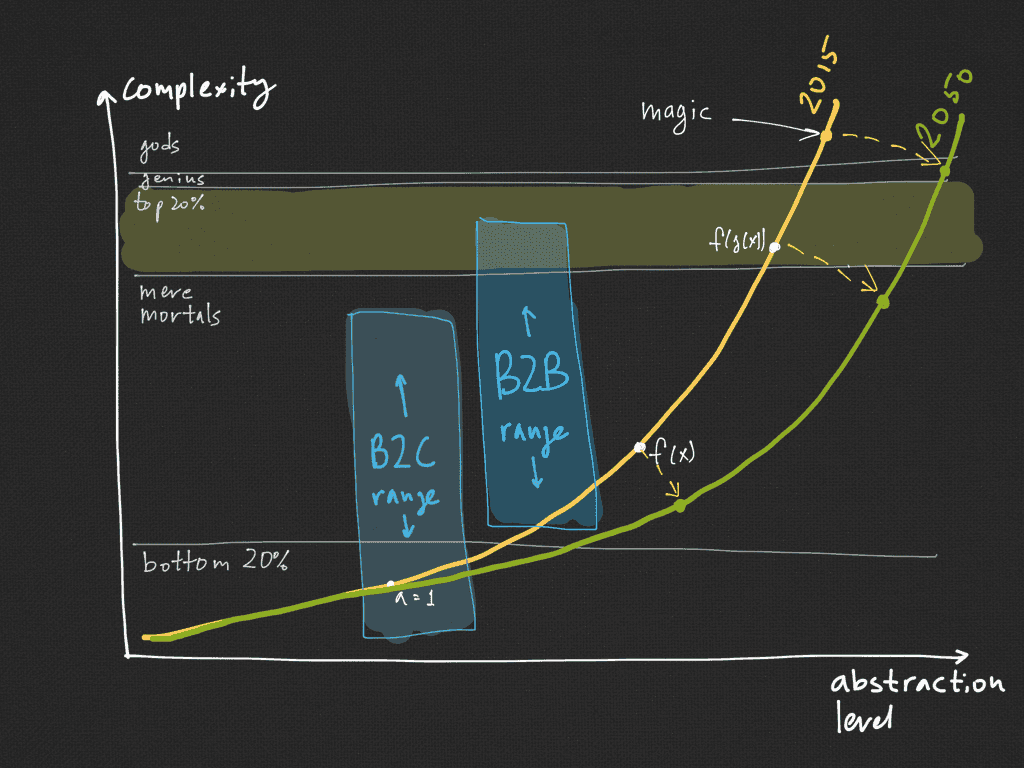
Let’s create a graph that will show how complexity and abstraction are linked together. I believe the graph will look like this (the horizontal lines are the division of humanity into groups according to their ability to perceive abstractions):

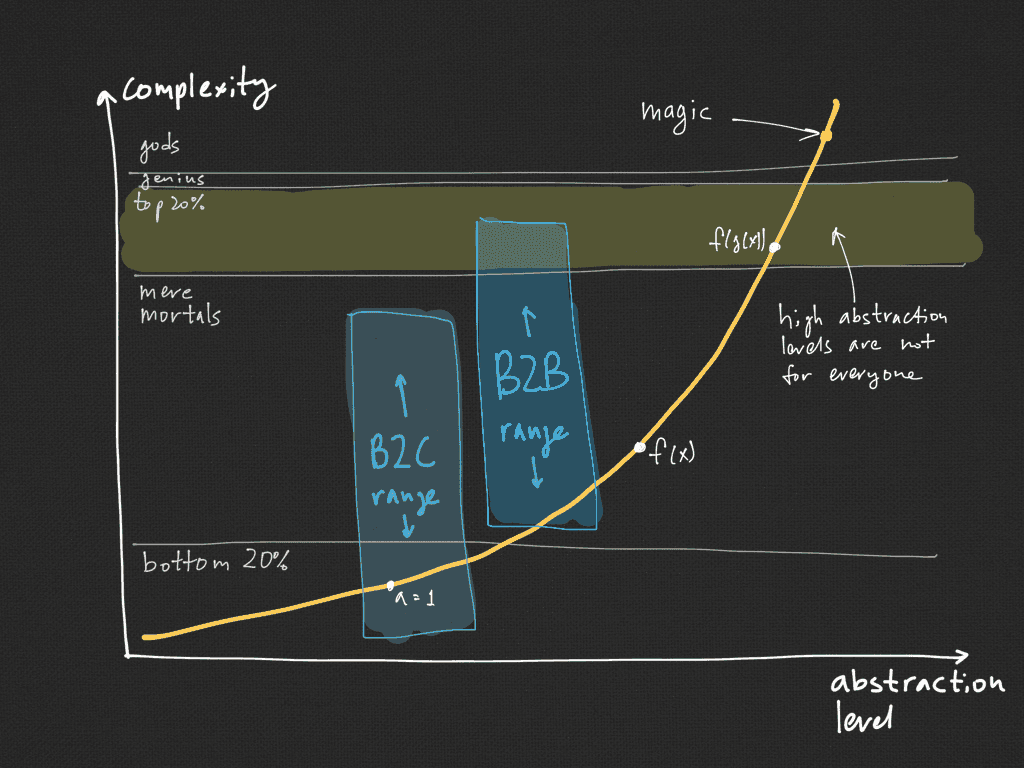
It’s clear that raising the level of abstraction complicates the understanding of concepts and systems. Initially, an increase in abstraction doesn’t greatly affect complexity. In fact, natural and rational numbers are quite close. Or, let’s say, variables and functions as well. But then there is a sharp jump and the complexity increases exponentially.

Higher-order functions are well understood by no more than 20% of programmers. Very few people understand the general theory of relativity at all. Even higher levels of abstraction are only accessible to geniuses, and at the highest level, the system turns into magic and is only understood by gods.

For ordinary mortal users, abstract systems should hide their abstractness and pretend to be concrete individual cases.

To delve into more or less abstract notions and concepts, one needs to make quite significant additional efforts. People generally don’t like to do this unless the reward is high. Therefore, if you are making business applications, you need to show everything very specifically and hide abstract things until the time comes.

Note: B2C solutions should work with lower levels of abstraction because most people simply won’t delve into anything more complicated than Instagram. B2B solutions are a bit freer in this regard but don’t expect that all business users are geniuses or in the top 20%.

Power

Increasing the level of abstraction enhances the power of the system. Indeed, more abstract concepts usually have greater predictive power and allow for more impressive feats. For instance, with the grammar of graphics, we can create almost any diagrams. The general theory of relativity predicted gravitational time dilation and the existence of black holes.

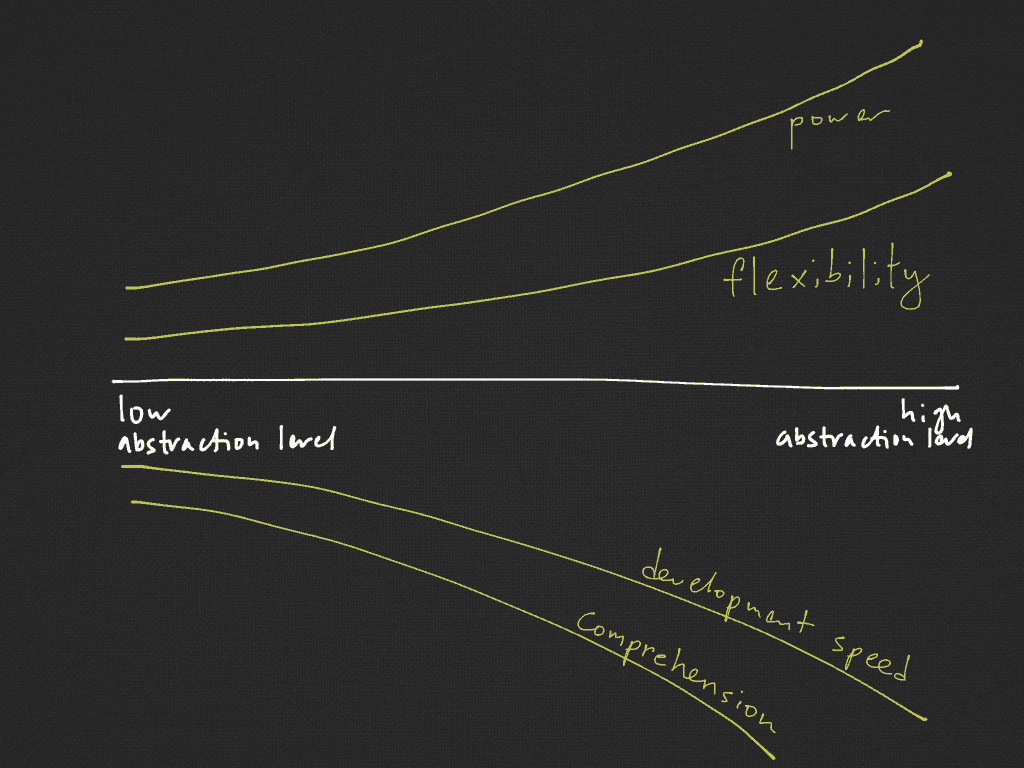
When applying all of this to software development, abstract systems are harder and longer to make. Choosing the correct level of abstraction to build a system is a critically important task. A high-level abstraction is slow, complex, and powerful, while a low-level is fast, simple, and specific. It should be noted that almost all decisions in custom software development operate at the lower level.

Creating useful and deep abstract concepts is an art.

Evolution

In my opinion, almost all systems in all areas evolve into increasingly abstract and complex forms. Most likely, software products are no exception.

However, the overall level of intelligence is growing and gradually more and more people are embracing more abstract concepts. For instance, what now seems like magic, will be understandable to geniuses in 40 years. And most programmers will finally learn how to properly use higher-order functions.

Generally, a familiar abstraction is rarely perceived as an abstraction. For example, no one considers the number 3 an abstract concept because it has become trivial over time. Most likely, the same will happen with other concepts.

The future of software development belongs to more abstract systems.

History tells us the same.